Exercícios de fração para 4º e 5º Ano
As frações são um dos conceitos matemáticos fundamentais que os alunos do 4º e 5º ano do ensino fundamental precisam dominar. Para ajudar no treinamento e aprimoramento desses conhecimentos, preparamos uma série de exercícios sobre frações, especialmente desenvolvidos para essas faixas etárias. Essas atividades são prontas para imprimir e podem ser aplicadas em sala de aula, proporcionando uma maneira divertida e interativa de aprender matemática.
Trabalhar com exercícios sobre fração permite que os alunos desenvolvam habilidades essenciais, como a compreensão dos conceitos de partes inteiras, numeradores e denominadores, além de aprenderem a realizar operações básicas com frações, como adição e subtração. A seguir, forneceremos algumas dicas úteis sobre como trabalhar com esses exercícios e estimular os alunos:
Dicas para Trabalhar com Exercícios de Fração
Explicação dos conceitos:
Antes de iniciar os exercícios, faça uma revisão dos conceitos básicos de frações. Explique o que são numeradores e denominadores, como identificar partes inteiras e frações adequadas e impróprias, além de ensinar a leitura correta das frações.
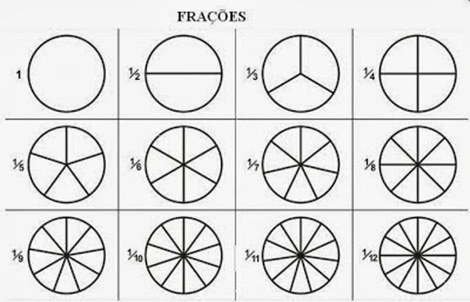
As frações são uma parte fundamental da matemática e são usadas para representar partes de um todo ou números que não são inteiros. Vamos revisar alguns conceitos básicos das frações para garantir um entendimento sólido.
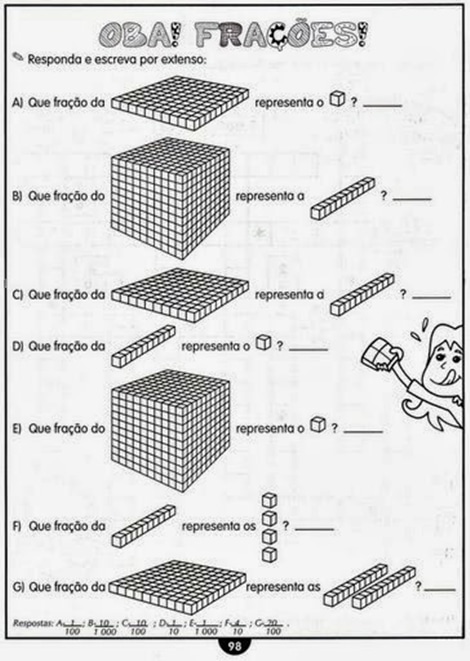
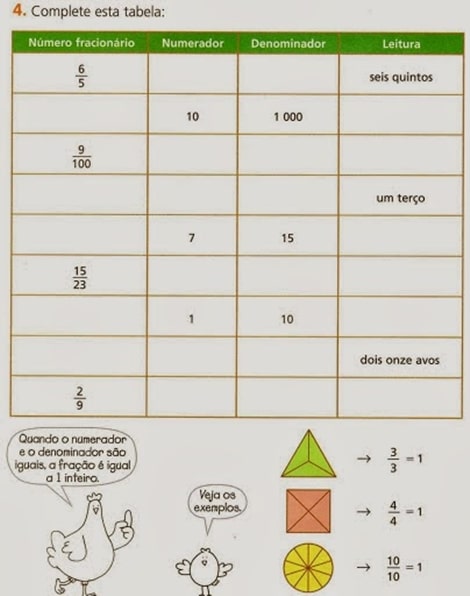
Numeradores e Denominadores: Em uma fração, o numerador e o denominador desempenham papéis importantes. O numerador representa o número de partes que estamos considerando, enquanto o denominador indica o número total de partes em um todo. Por exemplo, na fração 3/4, o numerador é 3 e o denominador é 4.
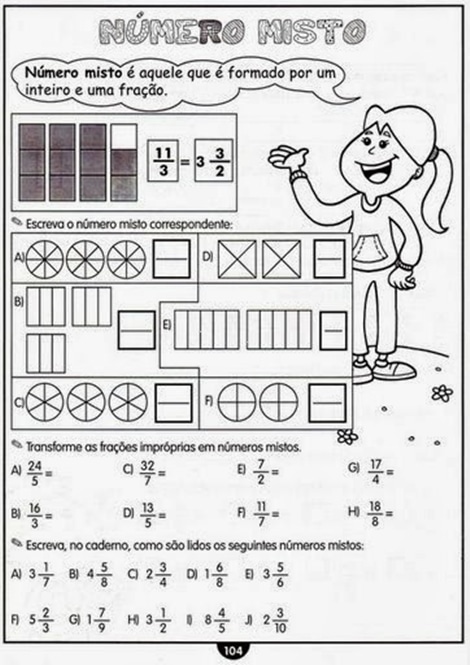
Partes Inteiras: Uma parte inteira é um número inteiro sem fração. Por exemplo, o número 2 é uma parte inteira. Quando temos uma fração que representa menos do que uma parte inteira, chamamos isso de fração própria.
Frações Adequadas e Impróprias: Uma fração é considerada adequada quando o numerador é menor do que o denominador. Por exemplo, a fração 2/5 é uma fração adequada, pois representa duas partes de um todo dividido em cinco partes iguais. Por outro lado, uma fração é considerada imprópria quando o numerador é maior ou igual ao denominador. Por exemplo, a fração 5/4 é uma fração imprópria, pois representa cinco partes de um todo dividido em quatro partes iguais.
Leitura Correta das Frações: Para ler corretamente uma fração, utilizamos o numerador e o denominador de forma específica. O numerador é lido como um número ordinal e indica quantas partes estamos considerando. O denominador é lido como um número cardinal e indica o número total de partes no todo. Por exemplo, a fração 3/5 é lida como “três quintos” e a fração 7/8 é lida como “sete oitavos”.
Revisar e compreender esses conceitos básicos é fundamental para o sucesso na resolução de exercícios de frações e na aplicação desses conhecimentos em problemas matemáticos mais avançados. Garanta que os alunos tenham uma base sólida nesses conceitos antes de avançar para atividades mais complexas.
Aplicação prática: Ao resolver os exercícios, incentive os alunos a relacionarem as frações com situações da vida real. Por exemplo, você pode utilizar objetos concretos, como fatias de pizza, para ilustrar a divisão de partes iguais e o conceito de fração.
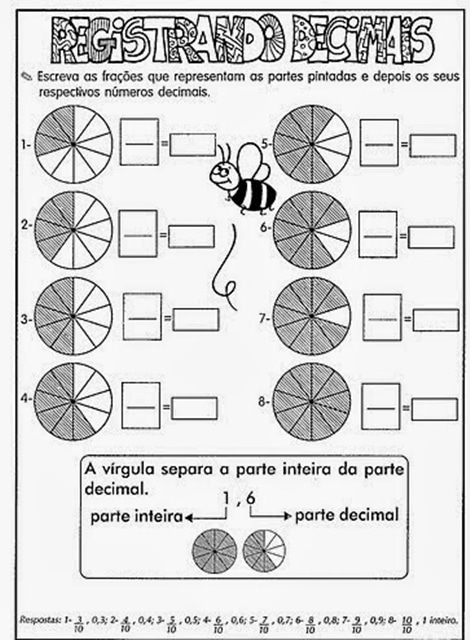
Uso de representações visuais: Utilize representações visuais, como diagramas de pizza ou retângulos divididos, para auxiliar os alunos a visualizarem as frações e entenderem como elas funcionam. Isso ajudará a consolidar o entendimento dos conceitos e a resolver os exercícios com mais confiança.
Estímulo à resolução em grupo: Promova atividades em grupo, onde os alunos possam discutir e resolver os exercícios juntos. Essa abordagem colaborativa permite que eles compartilhem estratégias, aprendam com os colegas e fortaleçam o trabalho em equipe.
Feedback e revisão: Após a resolução dos exercícios, forneça feedback aos alunos, destacando o que foi bem feito e oferecendo sugestões de melhoria. Reserve um tempo para revisar os conceitos-chave e tirar dúvidas, garantindo que todos compreendam plenamente os princípios das frações.
Ao utilizar essas dicas, você estará fornecendo uma experiência de aprendizado mais envolvente e eficaz para os alunos. Os exercícios de fração permitem que eles pratiquem e aprimorem suas habilidades matemáticas de uma forma divertida e desafiadora.
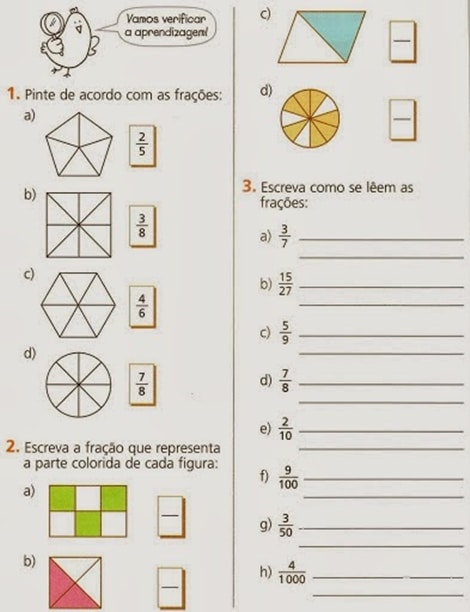
Atividades sobre fração para 4º e 5º Ano prontos para imprimir
Em conclusão, os exercícios de fração são uma ferramenta valiosa para o ensino e aprendizagem dessa importante área da matemática. Ao trabalhar com essas atividades, certifique-se de oferecer explicações claras dos conceitos, promover a aplicação prática das frações, utilizar representações visuais, estimular a resolução em grupo e fornecer feedback e revisão. Com essas estratégias, os alunos poderão desenvolver suas habilidades matemáticas de forma sólida e se tornarem mais confiantes em relação às frações.
Postagens relacionadas:
Exercícios de matemática 4° e 5º ano
Exercícios de português 5º ano para imprimir
